Artificial Spin Ice - Applications
In artificial spin ice structures there are a large number of magnetic configurations and, if they are to be used for computation, it is necessary to be able to access these configurations. In a first step, we show that small structures based on artificial square ice can be used to demonstrate deterministic and probabilistic forms of computing.
Traditional nanomagnetic logic utilizes dipolar-coupled nanomagnets, which have a magnetization that can be switched between two stable states acting as binary bits, to perform Boolean logic operations. Here we introduce a new perspective to computation with nanomagnets by incorporating ideas from the field of artificial spin ice.
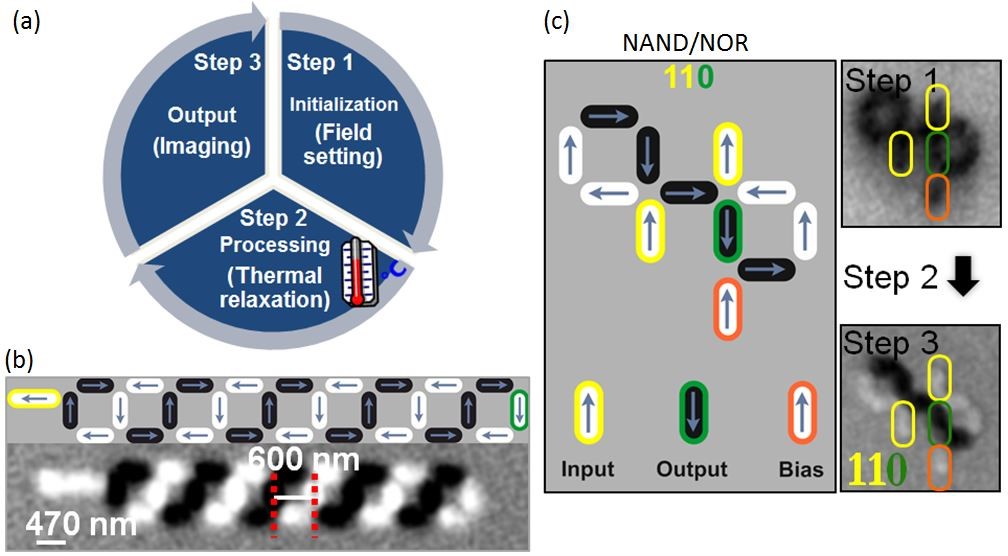
Computation was achieved via a three-step protocol as shown in Fig. 1a: (i) initializing the device by applying a magnetic field, (ii) heating the structure to allow it to spontaneously relax to a low energy state, corresponding to a particular logic operation, (iii) read-out of the performed logic operation using x-ray photoemission electron microscopy (X-PEEM). We experimentally demonstrated transportation of data in a chain of square rings made from Permalloy (Ni80Fe20) nanomagnets across large distances (>10 μm) and an X-PEEM image of one of the structures is shown in Fig. 1b. We also designed and tested Boolean logic gates on structures derived from artificial square ice (Fig. 1c). By carefully designing the relaxation pathways, i.e. the spin flips required to go from an initial state to a final output state, we could produce highly deterministic outputs and, with an operational reliability of >90%, the logic gates proved to be highly robust [1].
The introduction of metastable states into relaxation pathways can produce an outcome with a particular probability [2]. Such probabilistic outcomes could be implemented in weighted computational schemes such as artificial neural networks. An example of a logic gate producing probabilistic outcomes, which we refer to as a P-gate, is shown in Fig. 2. The P-gate is allowed to thermally relax following the scheme shown in Fig. 1a and, starting from the initial state shown in Fig. 2b, the gate thermally relaxes to the G1, G2 and M states with a given probability (Figs. 2c, d and e). A state network diagram indicating the relaxation pathways to G1, G2 and M states is shown in Fig. 2f.
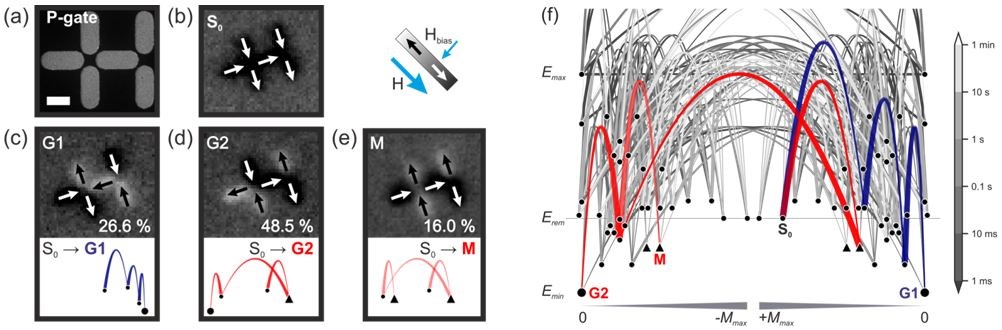
We have shown that the outcome of a logic gate can be adjusted by modifying the dipolar coupling strength and it should be possible to tune this outcome based on a feedback loop for use in probabilistic computation schemes. We have also demonstrated that several logic gates can be connected together, which could be implemented in extended computational circuits to perform Boolean algebra or perform probabilistic computation for image recognition.
The control of the motion of emergent magnetic monopoles in artificial spin ice is of interest for their use in devices. By modifying the design of an artificial square ice structure, monopole currents can be injected at specific locations, which results in a directional propagation [3].
References:
- Computational Logic with Square Rings of Nanomagnets
H. Arava, P.M. Derlet, J. Vijayakumar, J. Cui, N.S. Bingham, A.K. Kleibert, and L.J. Heyderman, external page Nanotechnology 29, 265205 (2018) - Engineering Relaxation Pathways in Building Blocks of Artificial Spin Ice for Computation
H. Arava, N. Leo, D. Schildknecht, J. Cui, J. Vijayakumar, P.M. Derlet, A. Kleibert and L.J. Heyderman, external page Phys. Rev. Applied 11, 054086 (2019) - Control of emergent magnetic monopole currents in artificial spin ice
H. Arava, E. Y. Vedmedenko, J. Cui, J. Vijayakumar, A. Kleibert, L.J. Heyderman, external page Phys. Rev. B 102, 144413 (2020)